HIDEAGEM is an experimental tool for hiding files inside of images using passwords. It’s written in C++ and can be used via CLI and with ComfyUI for Stable Diffusion.

About HIDEAGEM

HIDEAGEM is an experimental open source steganography tool for hiding data (Gems) of any kind inside of images.

It uses stong cryptography to make both hidden message extraction and decryption infeasible, and steganographic techniques that aim to minimize cover image mutation while maximizing data embed capacity.

It also employs potentially novel techniques in an attempt to mitigate password and key brute-force attacks.

WARNING: HIDEAGEM is currently experimental and may have unknown flaws or vulnerabilities!

This software is a work in progress: This article contains my current conclusions and observations, and they could change at any time.

To learn about HIDEAGEM’s basic technical details (software stack, feature list etc.) click here, otherwise continue reading to delve deep into its magic and lore! 🪄⚡

Once Upon A Time … 🕯️

This project began at the end of July 2023.

I’d been thinking about hiding data inside of images because of new content surveillance technologies that are being promoted (allegedly) for managing AI generated content online, such as Adobe’s C2PA “Content Credentials” (CR) tech.

Part of Adobe’s proposed content surveillance platform includes invisibly watermarking (hiding data inside of) all AI generated images using AI steganographic algorithms, the objective being to surveil the images' origin and nature.

That seems like a fun kind of magic to learn, doesn’t it ? ❤️

Hiding secrets in plain sight, woven inside of an image’s light! 🪄🎶

I hadn’t closely studied steganography or cryptography before, so I began my research and experiments.

I decided to study the simplest image steganography methods first, which are spatial domain algorithms that conceal message data directly inside of an image’s pixel bytes.

Stepping Into The Arena

After learning how to weave bits inside of images, development became focused on combining strong cryptography with the steganographic process in order to maximize security.

I entered the arena versus the Shadow Adversary ❤️: The hypothetical opponent who will try to steal our Gems! (Try to detect and/or extract hidden data from our magic images!)

After several months of wrestling with our beloved enemy, HIDEAGEM v.1 began to take form. 🐬✨

Core Magic Developed

💎 Mutable n-Bit Poly Key/RNG Hybrid Class: Integrating Argon2id-Derived 512-Bit Symmetric Keys and n-bit Keyfiles with XChaCha20-Based 256-Bit CSPRNG for Symbiotic Steganographic Data Embedding Using LSB Matching

An experimental key system and steganographic embedding algorithm are used in an attempt to leverage the full security of the cover media data embedding context.

Cover Media Data Embedding Context

Mutable n-Bit Poly Key / RNG Hybrid Class

Implementation of Key In Steganographic Data Embedding

💎 Dynamic Key Stretching Implemented Using Probabilistic Bitwise Encoded Metadata to Significantly Impede Password Brute-Force Attacks

Gem extraction metadata is encoded in such a way that any password guess decrypts valid metadata that defines dynamic key generation parameters with a high probability of increased computational cost for incorrect password guesses.

Probabilistic Bitwise Metadata Encoding Used to Implement Dynamic Key Stretching Space-Time Trap

💎 Ouroboros Cipher Stream Mutation: XChaCha20-based CSPRNG with O(1) Fast-Forwarding and n-Dimensional IV Generation

A CSPRNG is implemented that can generate 256-bit initialization vectors using n-dimensional coordinates for applications in non-linear and parallel procedures.

DragonRNG: 256-bit XChaCha20-based CSPRNG with Ouroboros Warp Mechanics

💎 Probabilistic Generation and Steganographic Embedding of Key Salt Bytes to Hinder Steganalysis and Password Brute-Force Attacks

A method that aims to hinder steganalysis and prevent steganalysis-based password brute-force early exit strategies.

Salt Generation with Probabilistic Steganographic Embedding

💎 Obfuscated Data Stream Metadata Encoding to Hinder Password/Key Brute-Force Attacks

A Method for encoding data stream byte counts such that any random 64-bit integer read from the cover media can be interpreted as a valid byte count that fits within the remaining capacity of the cover media.

Obfuscation of Data Stream Byte Count to Prevent Data Extraction Early-Exit

Gem Hide / Find Procedure

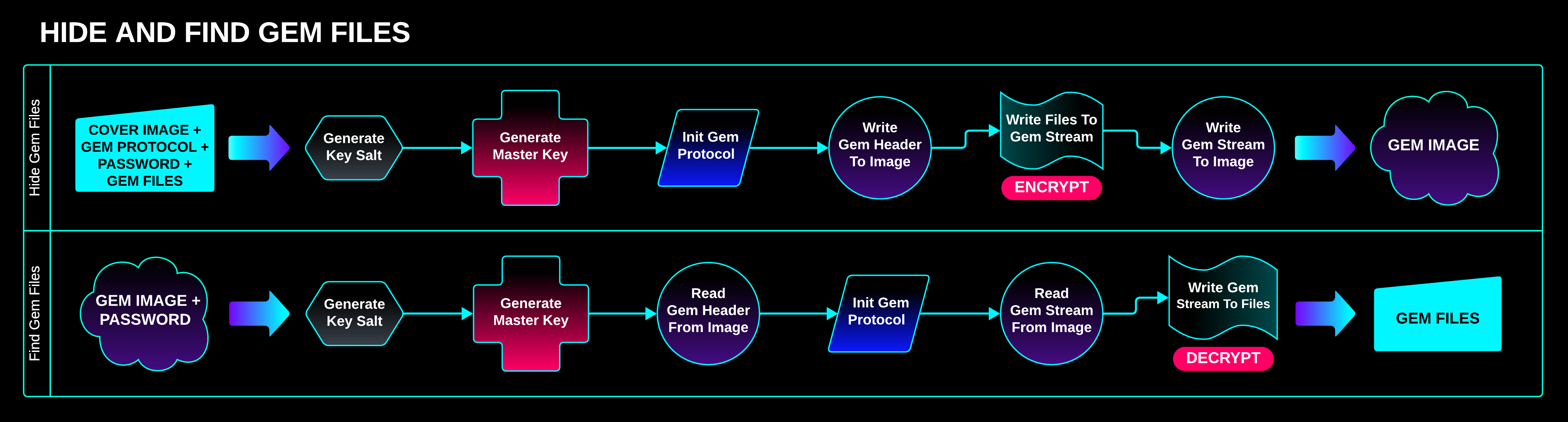
A cover image, Gem Protocol, password, and Gem Files are given to HIDEAGEM, and a Gem Image is produced.

The Gem Image contains the Gem Files, which are securely encrypted and hidden within the image’s pixels.

To extract the Gem Files, all that’s needed is the Gem Image and the password.

The Bit Ocean: Hiding Data Inside of Large Bit Collections

Hiding bits inside of an image is like hiding water in an ocean.

A steganographic procedure can not only encrypt the bits that will be hidden, but also shuffle them while embedding them in the cover media.

Consider a scenario in which an attacker wants to extract a hidden message from inside of an image:

• Step 1: Locate the hidden bits
• Step 2: Determine the correct order of the hidden bits

Let’s try to use ChatGPT to compute the minimum number of pixels required for 1-bit mode (1 bit of Gem data hidden per pixel) to exceed the search space of a 1024-bit key:

I’m not a mathematician, so I’m not able to verify if ChatGPT’s assessment is entirely correct. However, I think the takeaway is the following:

Brute-forcing the correct order of the bits extracted from the pixels is a daunting task at surprisingly small hidden message sizes.

In 1-bit mode the search space for brute-forcing the order of the bits exceeds that of a 1024-bit key at only 1030 pixels (~129 bytes), if the above calculations are correct.

For perspective, here’s how many universes of UNIFLOP scale computers would be needed to brute-force the bit order of 1030 pixels:

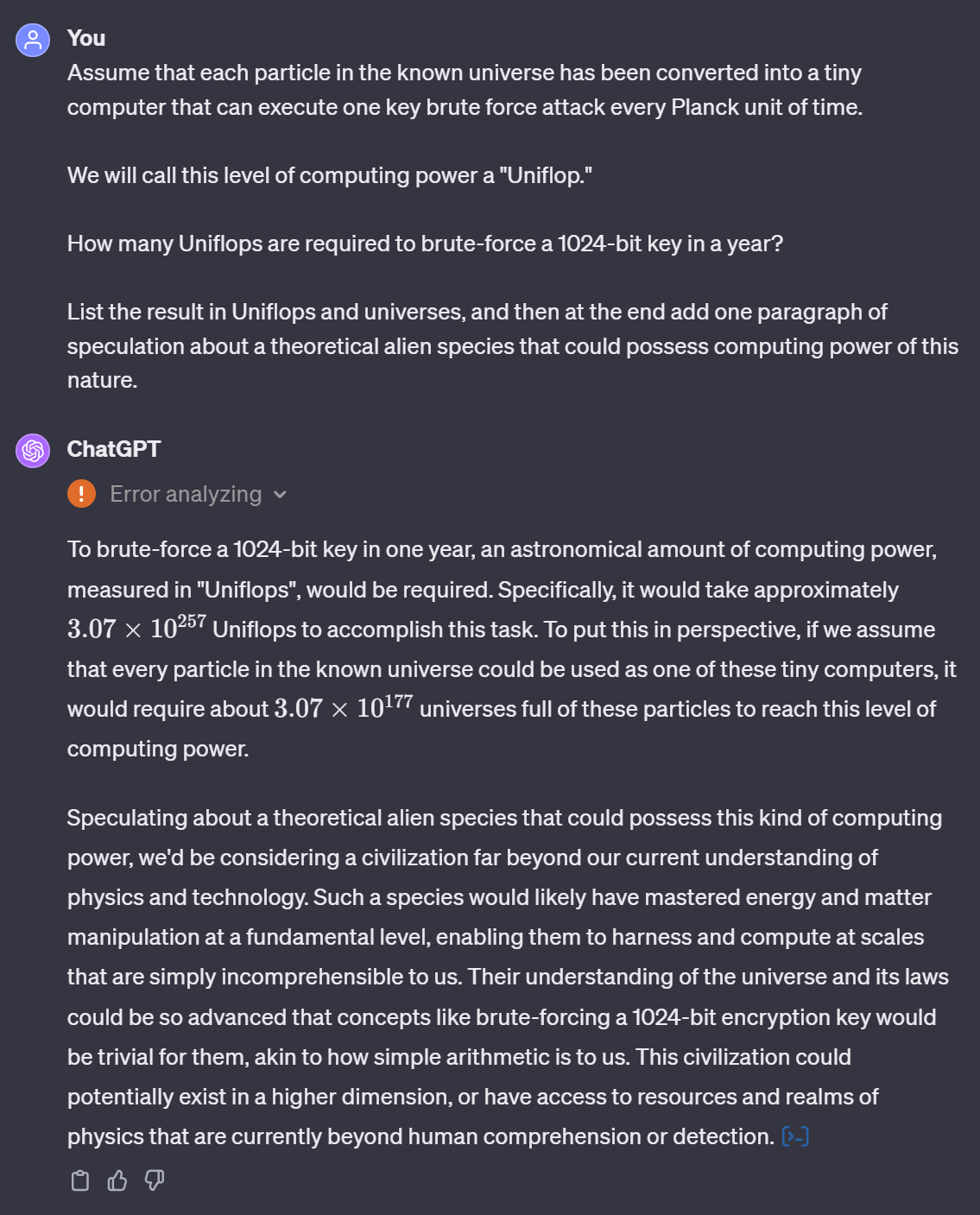
ChatGPT seems to be indicating that security at this scale is effectively xeno-hardened. 👽

Only celestial beings might be able to have a crack at stealing our Gems via this route! 💎🌌

The Key as the Weakest Link

Consider a scenario in which an attacker somehow knows the location of every pixel in the image that has hidden data embedded inside of it.

Assuming that:

• The attacker has extracted all of the bits from the cover media.
• That the bits cannot be distinguished from random.
• That generating a key has the same computational cost as generating a new permutation of message bits.
• The search space of the key used to generate the pixel order is less than the search space to brute-force the order of the message bits.

An attacker would focus on brute-forcing the key rather than the order of the message bits.

Maximizing Security Potential

HIDEAGEM is designed to embed/extract hidden data from cover images using a key derived from a password.

At some point, a symmetric key size (in bits) needed to be chosen.

While researching this, the usual advice I found is to use a 256-bit key, as it’s (currently) considered to be secure versus brute-force attacks done with a quantum computer. It’s also relatively easy to implement, as many cryptography libraries have functions that input/output keys of that size.

In the end, I decided to approach the decision as follows:

Implement a cryptographically secure key that can embody as many bits of entropy as possible.

While it’s true that passwords that have very high entropy are long and not easily remembered, I’d rather give users (now and in the future) as much freedom as possible.

Additionally, a system that can use larger (or even arbitrarily large) keys could later be adapted to work with keyfiles that exceed the size of a typical password.

HIDEAGEM Experimental Key System 🗝️🔥

Determined to investigate the possibility of implementing a key larger than 256 bits, I began my experiments.

I chose the libsodium cryptography library and its Argon2id password hashing function because it offers configurable resistance to offline password brute-force attacks.

I discovered however that using that library to implement a symmetric key size larger than 256 bits is a bit challenging, as all of the cryptographic functions HIDEAGEM uses accept a maximum key size of 256 bits.

What follows is an explanation of the key system I developed for HIDEAGEM, a proof of concept 512-bit (expandable) key implemented using the libsodium cryptography libary.

The Cycle Key

The Cycle Key is a class that securely generates, stores, and erases an Argon2id derived 512-bit key using a password and salt.

It also provides an RNG, the output of which is consumed internally by the Fire Key.

It’s been designed to work in concert with HIDEAGEM’s data embedding/extraction algorithms in order to encrypt the hidden message bits, as well as their location and order.

It is a poly key: The full security of the key is leveraged by cycling through two 256-bit key slices within the 512-bit key.

It is a mutable key: The key can consume bits to mutate itself unpredictably with entropy from its environment.

It is a hybrid key / RNG: The key contains an internal RNG and interface for using it, and consumes all of its cipher stream output.

512-Bit Key Generation

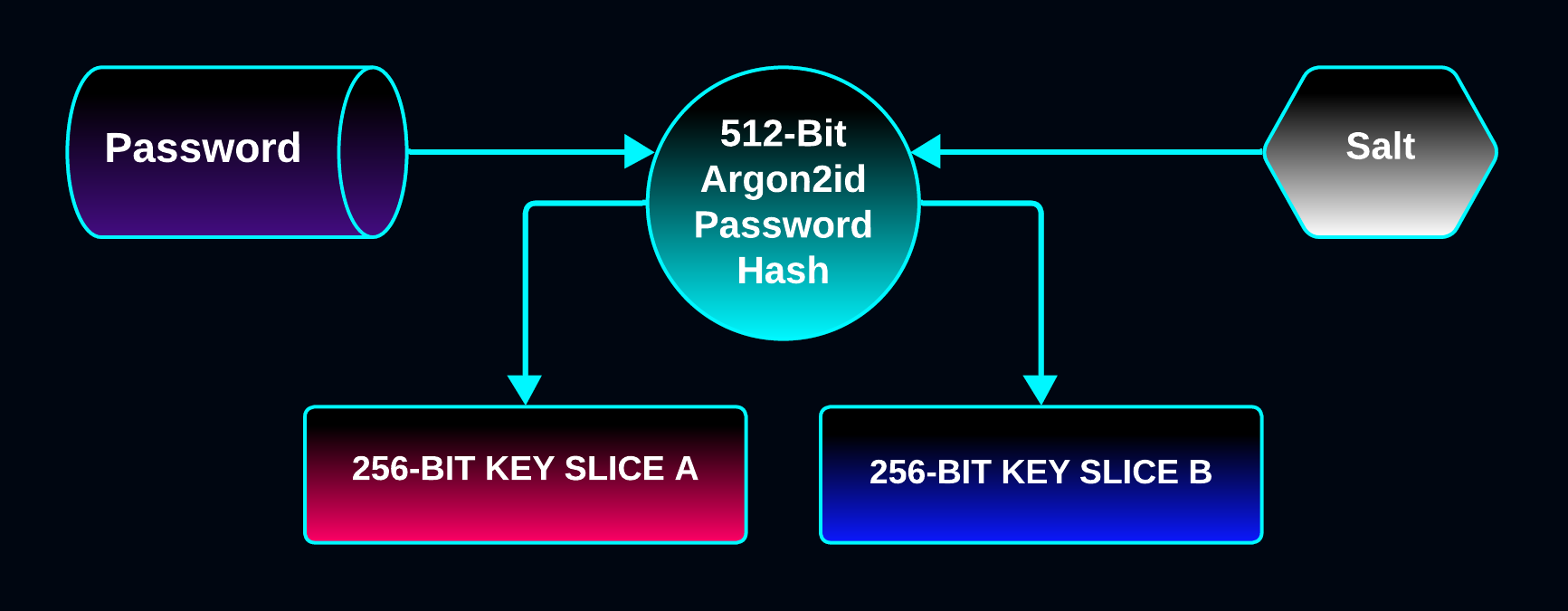
The 512-bit key is created by hashing the password with Argon2id into a 512-bit block that will be used as 256-bit key slices.

The key can embody a password’s entropy up to a maximum of 512 bits.

512 bits is the maximum number of bits of security Argon2id can provide, as 512 bits is the max digest size of the underlying BLAKE2b hash function.

The password hash is generated using libsodium’s INTERACTIVE key parameters (64 MB of memory).

Hybrid Key 🗝️ / RNG 🐍

The Cycle has an internal RNG that’s seeded with the Fire Key.

It provides an interface to the RNG for general purpose use, and the bytes of all random number output are consumed internally, causing the future state of the Fire Key to be influenced by how the RNG is used between cycles.

Each time the key is cycled with cycle(), the RNG is re-seeded with the new Fire Key.

The RNG is first initialized with the first 256 bits of the 512-bit key, then it’s used to shuffle the Fire Key slice order.

The Fire key slice order is re-shuffled with the RNG each time the random series of key slices are exhausted (so with a 512-bit Cycle Key, every second cycle will trigger a re-shuffling of the key slice order).

Consuming Key Food 🍖

The Cycle Key can consume bits from its environment in order to shapeshift.

It can be fed arbitrary bytes using its consume() function.

Each byte fed gets appended to a Food Pile vector, which gets hashed into a 256-bit Key Food array that is XORed with the current key slice to create the Fire Key each time cycle() is called.

Additionally, all random numbers output from the RNG’s cipher stream are consumed internally:

uint64_t rand_A = MASTER_KEY.rand<uint64_t>(); // Consumes rand_A internally (8 bytes)
uint64_t rand_B = MASTER_KEY.rand<uint64_t>(); // Consumes rand_B internally (8 bytes)

MASTER_KEY.consume( { rand_A, rand_B } ); // Consumes rand_A and B again

MASTER_KEY.cycle(); // Cycle to next key slice, consuming the Food Pile

In the above example:

• Two 64-bit integers are generated by the Cycle Key’s RNG.
• Those two integers' bytes are consumed internally (appended to the Food Pile).
• The same two integers are again consumed, this time by passing to consume().
• The Fire Key is cycled to the next 256-bit key slice.

When cycle() is called, the Food Pile is processed into the 256-bit Key Food array:

// Hash Food Pile into Key Food Array
void update_key_food()
{
    // Append curent Key Food to end of Food Pile
    // in order to incorporate previous state into hash
	food_pile.resize( food_pile.size() + KEY_SLICE_SIZE );

	std::memcpy(
		food_pile.data() + food_pile.size() - KEY_SLICE_SIZE,
		_key_food,
		KEY_SLICE_SIZE
	);

    // BLAKE2b hash food_pile into _key_food
    if (crypto_generichash(
        _key_food,
        KEY_SLICE_SIZE,
        reinterpret_cast<const unsigned char*>( food_pile.data() ),
        food_pile.size(),
        nullptr, 0) != 0 )
    {
        throw _E("Generic hashing failed while updating Cycle Key food array.");
    }

    food_pile.clear(); // Food Pile is now gone !
}

• The current Key Food array’s bytes are appended to the end the Food Pile, in order to incorporate the previous state.
• The Food Pile is hashed using BLAKE2b into the 256-bit Key Food array.
• The Food Pile is emptied.

Then the Fire Key is created by XORing the Key Food with the current key slice:

void update_fire_key()
{
	const uint8_t* fire_cycle = &_key[ KEY_SLICE_SIZE * fire_key_index ];

	// Copy current key slice into Fire Key
	std::memcpy( _fire_key, fire_cycle, KEY_SLICE_SIZE );

	// XOR Fire Key with Key Food
	for ( int i = 0; i < KEY_SLICE_SIZE; ++i )
	{
		_fire_key[i] ^= _key_food[i]; // Feed the fire
	}
}

• The next random 256-bit slice of the 512-bit key is selected.
• That slice is XORed with the Key Food array to produce the new Fire Key.
• The RNG is re-seeded with the new 256-bit Fire Key.

The state of the 256-bit Key Food array is influenced by all previous Key Food array states, the cipher stream output of the RNG, and any bytes explicitly fed to the key using consume().

This design allows for a mutable shapeshifting key to be easily reset to its initial state.

MASTER_KEY.reset_cycle(); // Reset Cycle Key to initial state

The key can also be set to auto cycle every n bytes consumed:

MASTER_KEY.auto_cycle( 64 ); // Activate auto cycle @ 64 bytes consumed

Now the key will automatically cycle each time the Food Pile’s size reaches >= 64 bytes (512 bits).

Control over the cycle rate relative to the byte consumption rate allows for fine tuning of the performance and security of the key’s implementation in a deterministic manner.

The n-Bit Fire Key 🔥

The Fire Key is a key that’s created by XORing the current key slice in the cycle with 256 bits of Key Food.

Each time cycle() is called on the Cycle Key, the key cycles to the next random key slice.

The Fire Key slice order is randomized by the internal RNG. Every two cycles, both slices of the 512-bit key are used, in a different random order each time.

The Fire Key can be mutated by feeding it arbitrary bits using the consume() function.

uint64_t ocean_index = MASTER_KEY.rand_range<uint64_t>( ocean_size - 1 );

std::vector<uint8_t> ocean_byte = read_ocean_byte( ocean_index ); // Read Gem pixel

MASTER_KEY.consume( ocean_byte ); // Consume cover Ocean bits and Gem bits
MASTER_KEY.cycle();               // Cycle to next key slice

In the above example:

• An RNG seeded with the Fire Key generates a random Ocean index
• A Gem pixel is read from the Ocean (contains Ocean bits and hidden Gem bits)
• The Ocean bytes are consumed by the Cycle Key (heaped on the Food Pile)
• The Cycle Key is cycled to the next random 256-bit key slice
• The Food Pile is consumed by the Fire Key
• The RNG is re-seeded with the mutated Fire Key

The Fire Key is used to generate the random Ocean byte locations where the Gem bits are hidden. It encrypts the location of the hidden message bits, as well as their order.

To implement it correctly, it must be impossible for an attacker to brute-force the key slices individually.

If the slices can be brute-forced individually, then the search space is only 2²⁵⁶ * 2 instead of 2⁵¹² (a vastly larger search space).

To learn about how HIDEAGEM implements the Fire Key, visit the GEMMA_RANDOM section.

Argon2id Key Regeneration

The Cycle Key can regenerate itself with the regenerate() function.

This causes the next 640 bits of output from the RNG to be used as the password and salt to regenerate the 512-bit key using the Argon2id password hashing function.

Regeneration is useful for implementing key stretching.

Secure Memory

libsodium’s low level memory management functions are used to store the key data in protected memory that won’t be swapped to disk, and to securely erase the key upon destruction.

Expandable Key: Support for Keyfiles

The Cycle Key could be used to hide Gems inside of images using files of any size as keys.

It can cycle through any number of 256-bit key slices, so keyfiles of arbitrary size could be substituted for the password-derived key, such as one-time-pads.

Another approach could be to combine a password with a keyfile, and have the Cycle Key consume the bits of the keyfile over time.

GEMMA_RANDOM Steganographic Algorithm

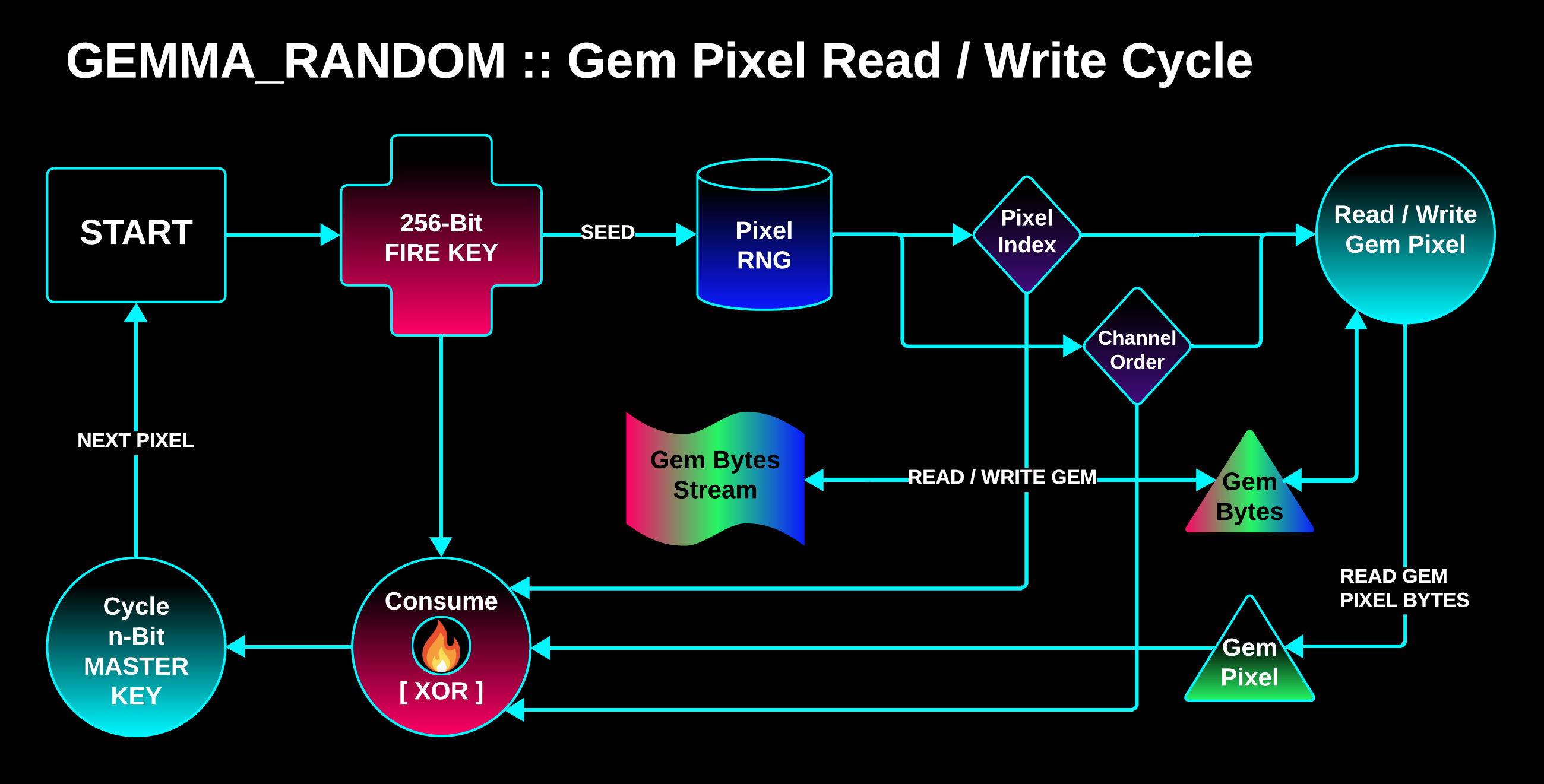
GEMMA_RANDOM (or GEMMA_R) is a spatial domain steganographic algorithm designed to force an unpredictable sequential read of bits when extracting Gems from an image.

It’s designed to make it impossible to extract any bits of Gem data without all 512 bits of the Cycle Key.

It can embed from 1 to 24 bits per pixel in one bit increments using a technique called LSB Matching.

GEMMA_R is designed to:

• Guarantee a unique random pixel set for every password + files + image set.
• Require all 512 bits of the Master Key to locate and read the pixels with hidden data.

This is achieved by using the Master Key’s Fire Key.

Procedure

The Gem Trail (sequence of pixels) is found by seeding an RNG at each visited pixel with the Fire Key, which is mutated by consuming the pixel’s bits as well as the random numbers emitted from the RNG.

Each pixel visited:

• An RNG is seeded with the Fire Key and it emits a random pixel index and random order to read/write the pixel’s color channel bytes.

• The Gem data is written to or extracted from the pixel.

• The random numbers used and the Gem Pixel’s bytes are consumed by the Fire Key, mutating its bits.

• The Master Key is cycled to the next random 256-bit Fire Key slice.

The Fire Key for each pixel will be one of two different 256-bit keys that are cycled through in random sequence inside of the 512-bit key, mutated by all of the bits it has consumed so far.

It consumes the bits of the cover image, the Gem File, and the pixel’s RNG output in order to mutate itself unpredictably and uniquely for each key + image + file data set.

As a result:

• The same password will produce a unique random pixel set for each combination of cover image and Gem data.

• The entire 512-bit key is required to visit all of the pixels and extract the data.

The next pixel in the Gem Trail sequence cannot be located until the current Gem Pixel is read and the Fire Key is mutated.

Additionally, the 192-bit true random nonce that’s used to encrypt the Gem Stream is appended to the very end of the stream, which makes it infeasible to decrypt any extracted Gem bits until the entire stream has been extracted, even with the right key.

Adversary vs. GEMMA_RANDOM

Consider a scenario in which an attacker is trying to brute-force the 512-bit Master Key directly in order to steal a Gem.

When a brute-force attempt fails, the attacker gains no information about which 256-bit slices of the key were valid or invalid, as the data extracted from the image at each visited pixel is indistinguishable from random.

The only way to discover that any single 256-bit slice of the 512-bit key is valid is for both slices to be valid simultaneously, which can only be confirmed by visiting all pixels in the correct sequence, extracting the Gem bytes, and successfully decrypting the bytes.

Even if an attacker somehow guesses 511 bits of the key and the initial key slice order, they would:

• Only be able to extract Gem bits from at most one pixel.^[1]

• Have no way of knowing that the bits are Gem bits.

• Not be able to decrypt any of the bits.

• Have no way of knowing if any of the 256-bit key slice guesses were correct.

The last point is key^;): The key slices cannot be brute-forced individually.

If any bit in the key is not a match with the actual key, the data extraction immediately diverts into random pixels and the procedure fails.

It’s for that reason that the Cycle Key’s search space is 2⁵¹² bits instead of 2²⁵⁶ * 2 (a much smaller search space) when implemented in this manner.

[1]  They would be able to extract ZERO Gem File bits, as the entire 512-bit key
     is needed to read the Gem Header before Gem File extraction can begin.

Update

The GEMMA_RANDOM section was written before the Cycle Key’s auto cycle feature was thought of, and some other changes to the program were made. I’ll leave the version above since it fundamentally describes the same exact process.

Now, instead of cycling the key every pixel, it auto cycles after the Food Pile contains at least 64 bytes (BLAKE2b’s max hash digest size), and instead of selecting random pixels (3 bytes at a time) it now selects random individual bytes in the Bit Ocean (a bit collection, such as an image or audio file).

Demo

A demo of GEMMA_1R .. 24R embedding close to the max message capacity for each bit mode + image size.

In order to minimize visible image mutation, the least significant bits (LSBs) of the pixel color channel bytes are written to first, distributing them evenly across all channels.

The smallest bit mode that can write all of the Gem bits in a single pass is auto-selected based on the final Gem Stream size.

Bit modes that cause a lot of visible mutation aren’t very practical in terms of trying to hide the presence of a message; nevertheless, the algorithm can write to all of the bits in a pixel.

LSB Matching

All bits written to the cover image are written using a technique called LSB Matching , which is distinct from and superior to a technique called LSB Replacement in which the least significant bits of the pixel’s color channel bytes are simply replaced with the hidden message bits.

LSB Replacement causes easily identifiable statistical anomalies that are exploited by steganalysis tools.

LSB Matching instead randomly adds or subtracts a value from the pixel channel byte (being careful to avoid overflow/underflow, which can cause extreme pixel mutation) so that the relevant least significant bits of the byte will match the hidden message bits.

True Randomness Source: It’s worth noting that the true random add/subtract of each Ocean byte write operation adds a significant amount of randomness to the Ocean byte / pixel randomization during the embed process, due to the fact that the Cycle Key consumes the Ocean byte after it’s written to.

Performance and Requirements

GEMMA_R can embed and extract data relatively quickly; it should be suitable for interactive contexts where users are frequently hiding and extracting data in/from cover bit collections.

It’s compatible only with lossless image formats such as PNG and TIFF (the Gem Image must be losslessly encoded, the cover image can be any type).

Potential Variations

A multithreaded version of GEMMA_R (GEMMA_RM) could be explored that hides/extracts message bits using each slice of the Cycle Key in parallel.

This could potentially speed up message embedding/extraction significantly.

Alpha Channel Tricks

Experiments could be done to see if 24 bits of data can be hidden in the RGB channels of pixels that are fully transparent.

Robustness: Image Mutation

Mutating the Gem image after embedding data can make the data unrecoverable:

• Resizing the image any amount: Complete data loss
• Re-encoding image (e.g. PNG to JPEG): Complete data loss
• Mutating pixel colors: Complete data loss if any Gem pixel mutated

The more data is embedded, the more fragile the Gem image becomes in terms of potenially surviving random pixel corruption.

Robustness: Steganalysis

Some simple preliminary tests using the well-named steganalysis tool Aletheia (Greek goddess of truth) seem to indicate that GEMMA_R in 1-bit mode may perform close to what’s expected for an algorithm that employs LSB Matching.

More comprehensive testing to measure steganalysis robustness will be conducted in the future.

🚨 Be aware that the data embedding threshold before detection by such tools is relatively low.

For example, while testing with a 1024 x 1024 cover image, Aletheia consistently detected the presence of a hidden message once the message size exceeded around 11 KB.

Note however that the detection of a potential hidden message does not guarantee that an attacker can identify all of the pixels with hidden message bits.

Even if an attacker has the original cover image to compare with the stego image (so each mutated pixel can be identified), it’s possible (and often highly probable at small bit modes like 1 bit per pixel) that when embedding the hidden message the pixel’s bits don’t need to be mutated because they match the message bits.

Dragon RNG: Ouroboros Class Random Number Generator

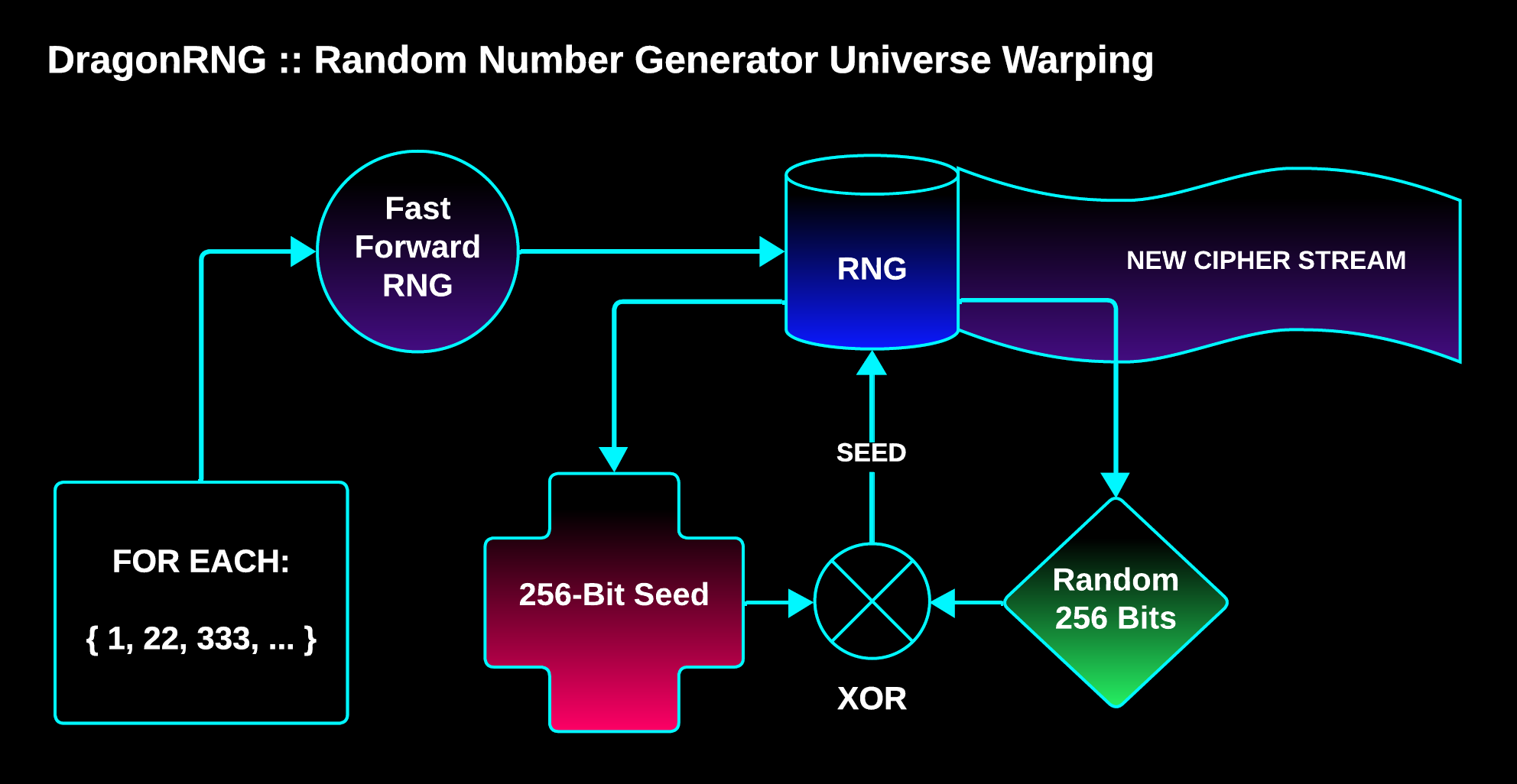
HIDEAGEM has its own cryptographically secure pseudo random number generator (CSPRNG) class called DragonRNG that’s implemented using the XChaCha20 stream cipher.

It can be fast forwarded in O(1) time, seeded with an array of bytes of any size (up to a max of 256 bits of entropy), and it can generate its own initialization vectors (it can warp to a new universe using warp coordinates).

It warps to a new universe (creates a unique stream of random numbers) by eating its own tail:

// Warps to cipher stream universe at coord:
//
// - Fast forwards WARP_STRIDE * coord bits
// - Creates a WARP SEED by XORing seed with the next SEED_SIZE bits from the cipher stream
// - Replaces this RNG with one seeded with the WARP SEED
//
// The RNG eats its own tail and vanishes from this universe, warping to a new one!
void warp( const uint64_t coord )
{
    fast_forward( coord * WARP_STRIDE );
    warp(); // Warp to new universe!
}

// XOR seed with next 256-bits of the cipher stream and
// replace self with new RNG seeded with the mutated seed.
void warp()
{
	// Create WARP SEED by XORing seed with next 256 bits of cipher stream
	auto warp_seed = seed;

	for (auto& byte : warp_seed)
	{
		byte ^= rand_byte();
	}

	// Replace this RNG with a new RNG seeded with WARP SEED
	initialize( warp_seed ); // ( the snake eats its own tail )

	// Secure erase WARP SEED
	sodium_memzero( warp_seed.data(), warp_seed.size() );
}

An RNG can be warped using an array or vector of integers, where each integer is a warp coordinate.

For each warp coordinate, the RNG is fast forwarded to that location in the cipher stream, and then the next 256 bits of the cipher stream are XORed with the RNG’s current seed (it eats its own tail), creating a Warp Seed. The RNG is then replaced with a new RNG seeded with the Warp Seed.

This feature is quite useful for creating unique cipher streams using a single seed.

When seeding an RNG and using the RNG’s output for different purposes, it’s important to not re-use any of the RNG’s cipher stream (random number output) in order to maintain maximum security.

What if you want to create/seed RNGs on the stack as needed instead of sharing a single RNG instance?

For example, what if you want to use the same RNG in different threads, and it’s not easy to fast forward passed numbers used by one task because it consumes an unknown number of bytes from the RNG’s output stream?

Using warp coordinates, unique streams of random numbers can be created for different tasks using the same initial seed.

///
//    RNG WARP COORDINATES

constexpr RNGWarp<2> THREAD_A_WARP   = { 0, 0 };
constexpr RNGWarp<2> THREAD_B_WARP   = { 0, 1 };
constexpr RNGWarp<1> XOR_STREAM_WARP = { 1 };

. . .

///
//    INITIALIZE RANDOM NUMBER GENERATORS

DragonRNG rng_A   = DragonRNG( seed, THREAD_A_WARP );
DragonRNG rng_B   = DragonRNG( seed, THREAD_B_WARP );
DragonRNG rng_XOR = DragonRNG( seed, XOR_STREAM_WARP );

In the above example, two 2D warp coord sets and a 1D set are used to initialize three RNGs for different purposes, using the same seed.

For each unique seed + warp coordinate set, a unique cipher stream is created.

Best Practices

The following is a bit confusing, but preventing cipher stream reuse is important for cryptographic security.

In order to avoid accidental cipher stream reuse as both warp coordinates and random number output, it’s important to ensure that intermediate warp coordinates are not used as terminal warp coordinates, and vice versa.

For example:

constexpr RNGWarp<1> BAD_WARP_1    = { 0 };
constexpr RNGWarp<2> THREAD_A_WARP = { 0, 0 };
constexpr RNGWarp<3> BAD_WARP_2    = { 0, 0, 1 };

Here, BAD_WARP_1 will produce a cipher stream the first 256 bits of which will be used as warp coordinates for THREAD_A_WARP, meaning that the first 256 bits of the cipher stream output of warp { 0 } will be used more than once (both as random numbers and as warp coordinates).

Similarly, BAD_WARP_2 will use the first 256 bits of the { 0, 0 } warp (which is used by THREAD_A_WARP as random number output) in order to warp to the next universe.

Instead, the warps could be coded as:

constexpr RNGWarp<1> GOOD_WARP_1   = { 0 };
constexpr RNGWarp<2> THREAD_A_WARP = { 1, 0 };
constexpr RNGWarp<3> GOOD_WARP_2   = { 1, 1, 0 };

Here, warp { 0 }, { 1, 0 }, and { 1, 1, 0} are only used as a streams for random numbers, and warps { }, { 1 }, and { 1, 1 } are only used as warp coordinate streams.

The simplest way to avoid stream reuse is to just use 1D warp coordinates with unique coords:

constexpr RNGWarp<1> GOOD_WARP_1   = { 0 };
constexpr RNGWarp<1> GOOD_WARP_2   = { 1 };
constexpr RNGWarp<1> GOOD_WARP_3   = { 2 };
constexpr RNGWarp<1> THREAD_A_WARP = { 3 };

All of these warps will produce unique initialization vectors for random number generation, without reusing any cipher stream bits.

Generating the Key Salt

In order to mitigate precomputed key attacks and add randomness, a unique salt is generated so that the same password won’t generate the same key each time it’s used.

HIDEAGEM derives a salt using the password, several cover image pixels, and true randomness.

Procedure

An RNG is seeded using a hash of the password, then 16 bytes are read at random from the cover file (bit Ocean). There’s a true random chance each salt byte will be randomly “corrupted” and written back to the Ocean (see below).

The salt is generated by concatenating the bit Ocean size, the 16 bytes read from the Ocean, and the 16 random Ocean byte indices, then hashing them into a 16 byte (128-bit) salt using BLAKE2b.

The RNG is warped using the salt bytes as warp coordinates in order to randomize the salt byte locations in the bit Ocean.

The 16 salt bytes are reserved so that they won’t be mutated when hiding the Gem, ensuring that the same salt can be fished out of the Ocean during Gem extraction.

The password, bit Ocean properties, and true randomness are thus used to derive a salt that is usually unique not only for each password and image combination, but each time the same password is used with the same image.

Key Generation Early Exit Mitigation: Random Byte Mutation

Before collecting the salt bytes, they may be true randomly corrupted in order to mitigate a potential attack that could speed up password brute-force attempts.

// Read bytes from Ocean into salt hash data vector
for ( uint8_t i = 0; i < NUM_SALT_BYTES; ++i )
{
	// Ocean byte index key generated by RNG
	const uint64_t salt_ocean_index = get_rand_ocean_byte_index( rng );
	append_uint64( salt_ocean_index ); // Append random number to salt pile

	GemByte salt_byte = read_ocean_byte( salt_ocean_index );

	// Randomly corrupt salt bytes (only when hiding Gem, not finding)
	if ( !b_lock_ocean_write && true_random_rng.rand_bool( rand_corruption_rate ) )
	{
		// Ghost Vector secure erases itself upon destruction
		const uint8_t corrupt_byte = true_random_rng.rand_byte();

		salt_byte = write_bits_to_byte(
			salt_byte,    // Ocean byte
			corrupt_byte, // Corruption bits
			GEM_BIT_MODE  // Num LSBs to write
		);

		write_ocean_byte( salt_ocean_index, salt_byte ); // Write mutated byte to Ocean
	}

	salt_pile.push_back( salt_byte ); // Add salt byte to hash data array

	rng.warp( salt_byte ); // Warp RNG !
}

Consider a scenario in which an attacker knows exactly which pixels in the image have been mutated (perhaps they have access to the cover image, or an advanced steganalysis tool). ^[1]

If a password brute-force attempt selects salt pixels that have been mutated (have Gem data embedded) then the attacker can early exit before generating the Master Key, since salt pixels are reserved (write protected).

Such an early exit opportunity could offer massive speed ups in password brute-forcing attempts, as the primary cost of each attempt is incurred at the key generation stage.

The solution: (True) randomly corrupt a random number of salt pixels before hashing their bytes using the same bit mode as the selected Gem Protocol.

That way, an attacker cannot early exit before generating the Master Key based on which set (mutated or not mutated) any salt pixel is in.

Ideal Corruption Rate

Corrupting the salt pixels true randomly may not be enough.

It may be better to corrupt them at a rate relative to the amount of data being embedded in the image. More research is required.

The salt pixel corruption rate can be changed in the future without breaking backwards compatibility.

[1] In reality, even if an attacker has the cover image to compare with the Gem image,
    they may not be able to identify all of the Gem pixels, as the Gem data bits
    sometimes randomly match the pixel's bits.

Additional Observations

Reserving the salt pixels before hiding/finding Gem data in the image using a BLAKE2b hash of the password as the RNG seed causes problems for an attacker who somehow has the 512-bit Master Key but does not have the password.

When HIDEAGEM selects the next random Ocean byte to visit, the set of reserved bytes is excluded. If the salt bytes are not in the reserved bytes set (because the password was not used to generate them), then there is a chance that during extraction a salt byte will be randomly selected.

If this happens, the Gem Stream extraction will fail after collecting an unknown number of invalid bits from the Ocean, and the attacker will have no way of knowing which byte was the last valid byte visited (if any).

The Gem Header

The Gem Header is 32 bits long and contains:

• HIDEAGEM Version: First 16 bits
• Gem Protocol Key: Last 16 bits

After the Master Key has been generated, the Gem Header is the first thing written to and read from the bit Ocean during the embedding and extraction processes.

In regular mode, the Gem Header acts as a gate: Gem Find/extraction fails immediately after reading the Gem Header if an incorrect password is entered.

Gem Protocol Key

The Gem Protocol Key is a 16-bit signed integer value that defines the exact procedure that’s used to hide/find Gems in a cover Ocean. It specifies the stego algorithm to use, how to handle the Gem Stream, and anything else that’s required.

Current Gem Protocols:

• Key 0 activates AUTO MODE: The Gem Protocol is automatically selected based on the Gem data and cover Ocean.

• Key 1 is GEMMA_RANDOM 1-bit to 8-bit spatial domain algorithm.

• Key 2 is RUBY_TIME_TRAP special Gem enchantment.

Gem Protocol 0 (AUTO MODE) isn’t written to the Gem Header, but is used during the Gem Hide process to select a protocol.

Note that the 16-bit signed integer range is quite a bit larger than the number of protocols.

This is by design: The Gem extraction process is intended to fail after reading the Gem Header if the password/key is invalid.

Extraction failure at this stage improves the user experience e.g. when a user accidentally enters the wrong password. If the extraction didn’t fail at this stage, then it would fail after reading a random number of random bytes from the Ocean, which would waste the user’s time.

When the wrong password is used, random Ocean bytes are read and decrypted as the Gem Header, and the Gem Protocol Key will be a random number in the 16-bit signed integer range, meaning that the chance of a valid Gem Protocol Key being read with the wrong password is relatively low.

Each Gem Protocol can specify extra data to be fished out of the Ocean, such as key parameters and bit modes, that can also be validated.

Note that the Gem Protocol Key is not read until after the Master Key has been generated, meaning that an attacker trying to brute-force the password won’t know the password guess was wrong until after being forced to generate the key (which has a non-trivial computational cost).

Visit the Black Magic section for an alternative design that does not cause extraction to fail when random data is fished out of the ocean. 💞

HIDEAGEM Version

The version of HIDEAGEM used to embed the Gem data inside of the bit Ocean is a 16-bit unsigned integer.

It can be used in the future to provide backwards compatibility in the event a breaking change needs to be made to the program.

Reading/Writing The Gem Header

Both reading and writing the Gem Header is done after the Master Key is generated.

Write / Read

The Gem Header is encrypted and written to 32 random bytes in the cover Ocean one bit at a time.

Bit Mode

The Gem Header must be written and read in the same bit mode (number of bits written per pixel), and during extraction the Gem bit mode is not known until after the Gem Header is read.

This means that the same bit mode is used for all Gem Headers in all bit Oceans regardless of which bit mode is used for embedding/extracting the Gem data.

1-bit mode was selected as it’s the minimum amount any Gem Protocol can mutate a pixel when hiding data, which should help make it difficult to distinguish the Gem Header pixels from pixels that are mutated by the rest of the Gem data embed process.

Gem Header Random Mutation

It may be beneficial to true randomly mutate the bits in the Gem Header pixels up to the Gem Protocol bit mode before writing the header bits in 1-bit mode. That way, they may be even harder to distinguish from other Gem pixels.

This may be advantageous in some modes, and not in others. More research is required.

The Gem Stream

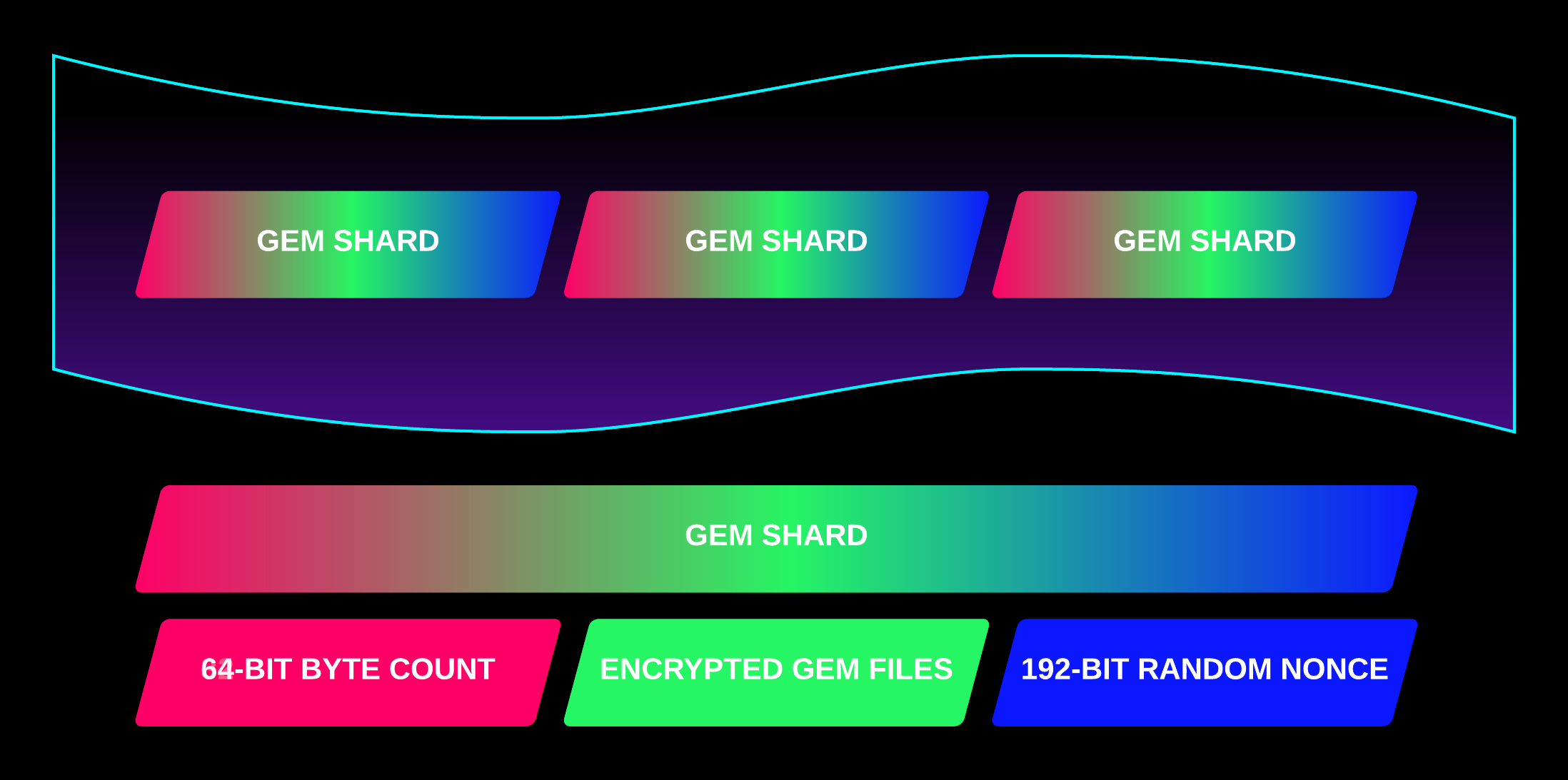
The Gem Stream is a stream of bytes made of Gem Shards.

It’s designed to be infeasible to decrypt before it’s been completely extracted from the Ocean.

This design property, preventing decryption of any of the hidden bits until all bits have been extracted, is a crucial prerequisite for other aspects of HIDEAGEM’s design.

This is accomplished by appending the 192-bit true random nonce to the very end of the Gem Stream, which is required (along with the Master Key) to decrypt any of the Gem Stream’s bits.

It’s also been designed so that every bit of the stream is indistinguishable from random, which is useful for many reasons.

A Gem Shard is composed of:

• Head: A 64-bit integer that stores the byte count of the Body.
• Body: The encrypted Gem bytes. Can be up to uint64_max bytes (16 exabytes).
• Tail: A 192-bit true random nonce used to encrypt the body.

The Gem Stream is created, written to, and read from the cover Ocean by the algorithms specified by the Gem Protocol.

Every bit of the Gem Stream is encrypted using a 256-bit key, a 192-bit true random nonce, and the XChaCha20_Poly1305 authenticated encryption algorithm.

Gem Shard Head

The first 64 bits of a Gem Shard is an integer that specifies the number of bytes to read from the Ocean as the Gem Shard’s Body.

The byte count is obfuscated so that no matter what 64-bit integer is fished from the Ocean, it’s interpreted as a number of bytes less than or equal to the remaining embed capacity of the Ocean.

The purpose of doing this is to make it impossible to early exit Gem extraction based on bits read from the Ocean with any key (or password).

The number of Gem bytes that can fit inside of a typical cover Ocean is much smaller than the 64-bit unsigned integer max value, so most random 64-bit integers would exceed the Ocean’s byte embed capacity.

A byte count that exceeds the Ocean capacity is invalid, so Gem extraction immediately terminates if one is read from the Ocean.

The Gem Shard’s byte count is obfuscated and de-obfuscated as follows:

///
//    OBFUSCATE AND ENCRYPT GEM SHARD BYTE COUNT

uint64_t XOR_KEY = rng.rand<uint64_t>();

// Pad byte count with random multiple of Ocean byte capacity and encrypt with XOR.
//
// Padding ensures that it can't be distinguished from a random number.
uint64_t max_multiple =
	( std::numeric_limits<uint64_t>::max() / byte_capacity ) - 1;

uint64_t padded_byte_count =
    byte_capacity * rng.rand_range( max_multiple ) + byte_count;

uint64_t encrypted_byte_count = padded_byte_count ^ XOR_KEY; // XOR

. . .

///
//    DECRYPT AND DE-OBFUSCATE GEM SHARD BYTE COUNT

uint64_t XOR_KEY = rng.rand<uint64_t>();

uint64_t decrypted_byte_count = ( encrypted_byte_count ^ XOR_KEY ) % byte_capacity;

In this manner, any random 64-bit integer fished from the Ocean is interpreted as a valid byte count (one that fits within the remaining capacity of the Ocean). 🐬 EE EEE EEE EE!

The byte capacity shrinks as Gem Shards are appended to the Gem Stream; the byte count is obfuscated relative to how much data has already been extracted from the Ocean.

Gem Shard Body

The Gem Shard Body is composed of the Gem data’s encrypted bytes, and can be up to uint64_max bytes long (16 exabytes).

It’s encrypted using a 256-bit key, a true random 192-bit nonce, and libsodium’s XChaCha20-Poly1305 encryption algorithm.

If any bits in the encrypted data have been tampered with, the decryption will fail.

The instant a Gem Shard’s Body fails to decrypt, the Gem Extraction terminates! 💥

Gem Shard Tail

The last 192 bits of the Gem Shard is the Tail: A 192-bit true random nonce that’s generated before encrypting the Body.

The true random bytes are XORed with a data whitening stream created with the Master Key in order to mitigate potential malfunction or compromise of the system’s randomness sources.

The nonce is intentionally appended to the end of the Gem Shard: It’s infeasible to decrypt any of the Gem’s bits until the entire Gem Stream has been read from the Ocean.

As a result, full extraction of the Gem bits from the cover media must be completed before decryption can be attempted.

This helps prevent known-plaintext attacks such as crib dragging, and helps ensure that the entire Cycle Key is needed to begin decrypting any of the Gem data.

The Gem Seal 💎♓✨

The Gem Seal is a unique legend that’s generated for each hidden Gem.

It describes a magical gemstone created at some point in the vastness of time, and is symbolic of the astronomical time scale required to steal a Gem using brute-force attacks! 🐬✨

Once a Gem hide/find completes, the final state of the RNG is used to generate the following:

• Gem Hash: A web-safe base64 string representation of the next 256-bits of the RNG’s cipher stream.

• Gem Seal: A unique legend generated using an RNG seeded with the next 256-bits of the RNG’s cipher stream.

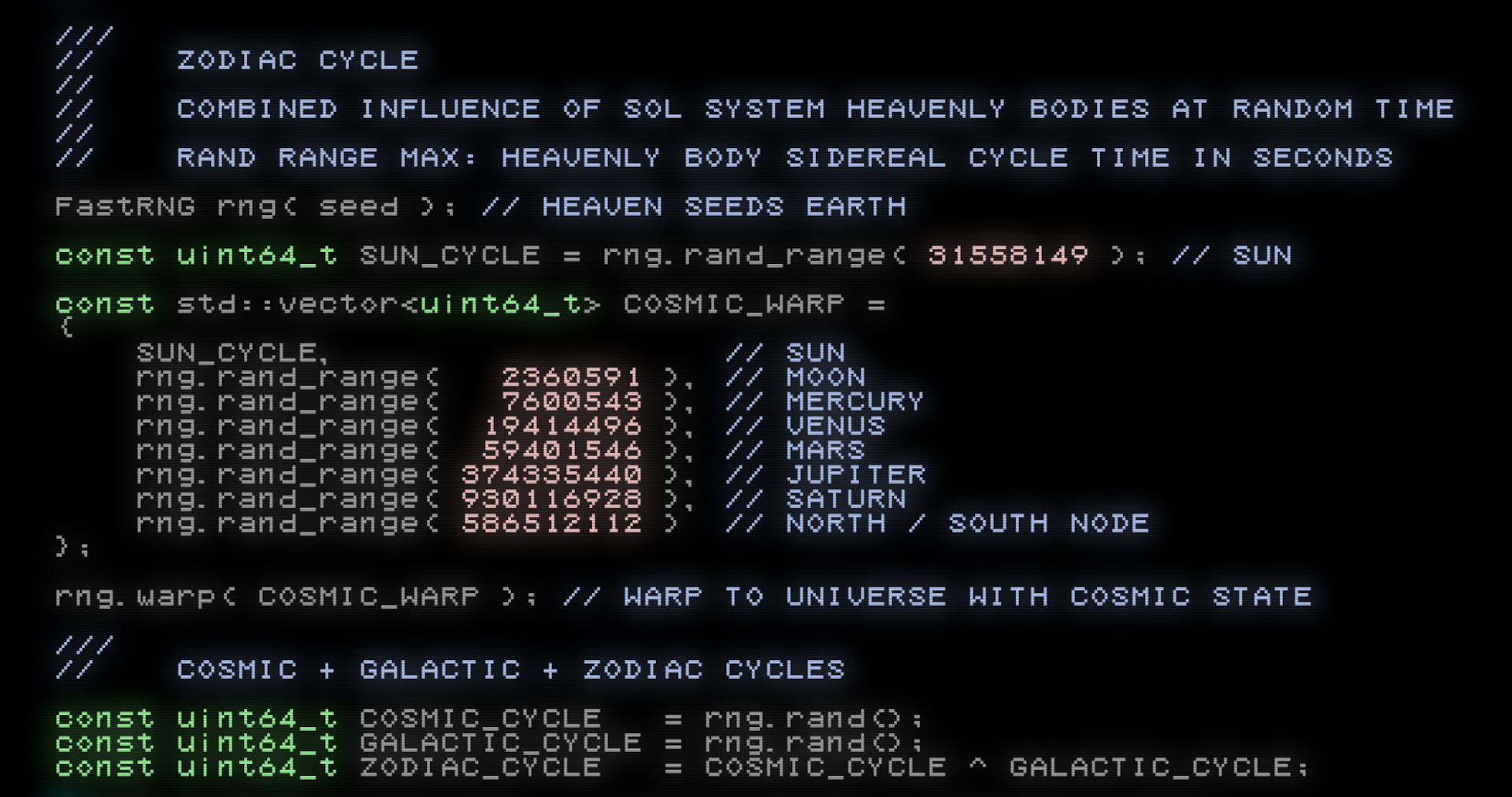
An RNG is warped to a universe with a random state of the heavens, and the Zodiac cycle and Gem properties are derived from it.

Each Gem has a ward, quality, gemstone type, element, and magic type.

Each Gem Seal also has a Gem Charm. 🧿

The charm is calculated by concatenating the 64-bit Cosmic cycle with the 64-bit Galactic cycle into a 1 .. 133-bit integer and recursively extracting its repeating digits until a number is computed that has no repeating digits. (There’s a little more to it than that, but you’ll have to peek the source code to see what I mean).

The charm level is a base 26 (A-Z) number that counts the number of times repeating digits are extracted.

It’s possible (and rare) for the charm number to overflow a 64-bit integer. This can happen when large sequences of repeating digits are present in the initial charm number.

When this occurs, the charm level gets the number of overflows appended to it after an asterisk:

e.g. CHARM [M*2] ...

An example of a massive (and very rare) Gem Charm.

The Gem Seal’s total number of permutations is unknown to me, and I actually have no idea how large a Gem Charm number can get.

For now I’ve coded it so that if the rollover exceeds 777 it just prints MIRACLE CHARM and the cosmic + galactic integer. If you ever see this please send me a screenshot!

Usage and Security Notes

A good use case is to share the Gem Hash with the intent to verify the integrity of a Gem. If when a user extracts the Gem they see the same Gem Hash, then it’s virtually guaranteed to be the exact same Gem.

The Gem Hash and Seal on their own won’t reveal anything about the image, hidden data, password, or key, so I want to say that they’re safe to share publicly.

However, since both of them can only be revealed when hiding or finding a Gem, posting them in the past could help prove that you (or someone else) hid or found a specific Gem at or before that time, so it can provide information in that regard. So be aware of the potential privacy implications.

It’s similar to sharing the hash of an unencrypted file along with the encrypted file. Only those with the decryption password can verify the hash.

Note also that each time the same password + image + file set is used, the Gem Seal will be different due to the true randomness introduced by the salt generation process and other sources.

Black Magic

Let’s explore some occult spells for hiding Gems even deeper within the mists of time! 🪄💕

In HIDEAGEM’s design, after the Master Key is generated the Gem Header is read from the image using the key.

If the Gem Header contains invalid data (e.g. because the wrong password was used) then the Gem extraction immediately fails.

The reason why a bad Gem Header is usually read from the image with an invalid password is because random keys are very unlikely to decrypt a valid one.

Instead, let’s consider a system that reads a valid data even if the password is incorrect, in order to cause a Gem extraction to be attempted anyways.

The idea is to make it impossible to tell if a password brute-force attempt is successful or not until after all of the bits are read from the image and decryption is attempted (the final step).

Can this be achieved, and could a system like this be used to increase the computational cost of brute-forcing the password or key?

A Magic Gem Protocol Key

The challenge: Encode the Gem Protocol Key in a series of bits such that any random series of bits can be interpreted as a valid Gem Protocol Key.

That way, even random bits read from the image with an invalid password will decrypt a valid Gem Protocol Key and the extraction will proceed.

The first idea I tried is the same technique that’s used to obfuscate the Gem Shard byte size:

• Obfuscate: Multiply the Gem Protocol Key by a random multiple of the total number of Gem Protocols
• De-obfuscate: Modulo the Gem Protocol Key by the number of Gem Protocols

This way, any random number read from the cover image can be mapped to a valid Gem Protocol Key.

The problem with using that method is that if more Gem Protocols are added in the future, then the number used to map the protocols changes and backwards compatibility is broken (won’t be able to extract Gems hidden with older versions of the program).

Consider the following alternative.

The Pit of Dolos – AKA The Bit Trap

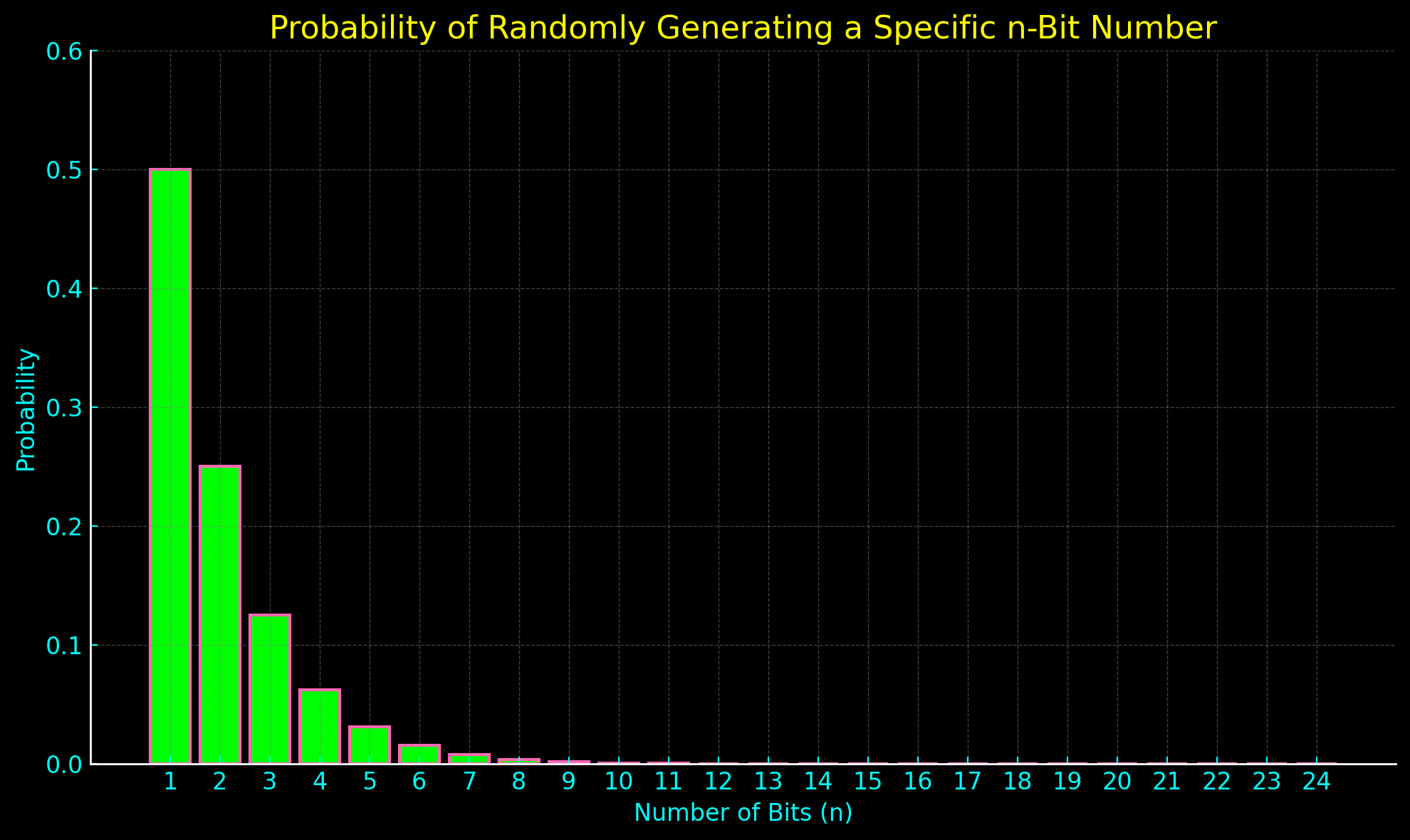
A series of bits can be used to encode the Gem Protocol Key such that the first non-zero bit’s index is the key value.

For example, consider these 8-bit numbers:

10101010 = Protocol 1 = 50%      (1/2)
01101010 = Protocol 2 = 25%      (1/4)
00101010 = Protocol 3 = 12.5%    (1/8)
00011010 = Protocol 4 = 6.25%    (1/16)
00001010 = Protocol 5 = 3.125%   (1/32)
00000110 = Protocol 6 = 1.5625%  (1/64)
00000010 = Protocol 7 = 0.78125% (1/128)
00000001 = Protocol 8 = 0.39062% (1/256)

This way, any random series of bits can be interpreted as a Gem Protocol Key (so long as at least a single 1 bit is read before the protocol max value is exceeded).

Additionally, it’s easy to expand the Bit Trap indefinitely; new protocols simply expand the maximum number of bits fished from the Ocean.

This system also has a peculiar property: The first index values are far more likely to be decrypted at random.

In fact on average, 50% of password brute-force attempts will decrypt index 1, as there’s a 50/50 chance that the first bit will be 1.

Decoding the bits this way creates an exponentially decaying probability of randomly reading higher index values.

Another way this could be done: A byte’s value 0 .. 255 could be interpreted with that same curve (or any other).

In the context of steganography, using the bit trap encoding instead could be useful, as writing a 1 to the first index has a 50% chance of requiring zero mutation of the cover Ocean (the bit may not need to be flipped).

Encoding the Gem metadata using a probabilistic algorithm like this opens up the opportunity for playing some beguiling tricks! 🐬

Poly Key Gem Protocols: Arbitrary Key Stretching Using Argon2id

What if the first Gem Protocols had a much higher computational cost than the rest?

That way, high cost protocols are nearly guaranteed to be activated for each password brute-force attempt.

To do that, we’d need a way to arbitrarily increase the computational cost of extracting a Gem, such as by employing key stretching.

This can be achieved by creating protocols that force Argon2id key regeneration every n Ocean bytes.

For example, regenerating the key every 1024 Ocean bytes can cause extraction of a few hundred KB of data to take over a minute.

What’s interesting about this, is that the fast protocols (if placed in the upper indices) are sort of “hidden” behind the increased computational cost of the slower protocols.

An attacker has no way of knowing if the password guess was correct until after the message extraction finishes and decryption is attempted, as the bits read from the image are indistinguishable from random.

On the one hand, an attacker might reason that if the protocol selected is slow, users are unlikely to use it to hide Gems, and simply abandon the brute-force attempt.

On the other hand, users may choose to use slow protocols for this very reason, since the increased brute-force cost could make it less likely for an attacker to bother trying.

Therefore, an attacker cannot rule out the possibility that a slow protocol was in fact used, and they’re forced to endure the minutes-long extraction in order to verify the password guess! 🐬💞

Time Trap Gems

HIDEAGEM’s first implementation of the bit trap is the Time Trap spell. 🪄

When hiding and fiding Gems the --timetrap parameter can be used to enchant the Gem with a trap that will slow down password brute-force attacks.

Time Traps have a level from 0 to 7 that changes how long it takes to extract the Gem and verify the password.

Level 0 has no additional time added: Gem embedding and extracting takes the same time as without a Time Trap.

Levels 1 - 7 have longer extraction times: 1 is the shortest and 7 is the longest.

When the correct password is entered, the Gem is extracted using the Time Trap level specified when hiding the Gem.

When an incorrect password is entered, a random Time Trap level is fished 🎣 from the Ocean with a high probability of catching the slowest one:

LEVEL 7 = 50%      (1/2)
LEVEL 6 = 25%      (1/4)
LEVEL 5 = 12.5%    (1/8)
LEVEL 4 = 6.25%    (1/16)
LEVEL 3 = 3.125%   (1/32)
LEVEL 2 = 1.5625%  (1/64)
LEVEL 1 = 0.78125% (1/128)
LEVEL 0 = 0.39062% (1/256)

Around half of password brute-force attempts will catch level 7, no matter which level was used to hide the Gem (even level 0).

It’s possible to hide Gems that take less than a second to extract with the correct password, but a wrong password guess takes several minutes to complete! 🐬 EE EEE EEE EE!

When a Gem has a Time Trap, the Gem Stream is configured so that its size isn’t known until after it’s been extracted, as a stop value is read from the end of a valid Gem Stream. That way, the only way to confirm a password guess was invalid is to read every byte in the Ocean!

For the Time Trap spell to be effective, the level it was cast at and the size of the hidden Gem must be kept a secret!

The price of the Time Trap is convenience: Accidentally entering the wrong password can cost a lot of time, so it’s not suitable for use in contexts where more immediate wrong password feedback is required.

Memory-Hard Gems and Space-Time Traps

A bit trap could be used to encode the memory parameters used for Argon2id key generation in order to create Memory-Hard Gems, which could add a space dimension to time trap spells.

Memory of nearly any amount can be specified: Gems could be hidden that require gigabytes of memory to extract.

Time Locked Gems

Gems can be locked behind a wall of time using huge space-time spells.

Large values could be used to make Gem extraction take hours, days, or even longer.

This spell could be used to time delay access to all sorts of things:

Scavenenger hunts and CTF competitions could use time locked Gems that take days to extract with a high-end consumer PC, adding computational resources as a factor in races.

Game developers could post time locked Gems on social media that contain passwords that unlock downloads or reveal secrets in games, and then gamers could race to try to extract them.

Summoning Hydra Gems

We can create a nightmare for would-be Gem thieves by summoning Hydra Gems! 🐍💎

Normally, HIDEAGEM encrypts Gem data using the XChaCha20_Poly1305 encryption algorithm, which includes a 128-bit data authentication tag.

After a password guess extracts a Gem Stream from the image, attempting to decrypt it will fail if it’s random data. At that point, the adversary discovers if the password guess was valid or invalid.

Instead of using an authenticated encryption algorithm, the Gem data could be encrypted using XChaCha20 alone.

The result would be that every password guess attempt would extract a random number of Gem Files (with random file names and random sizes) from the image, and the only way to determine if the password was correct would be to examine the output file(s).

Those random Gem Files could then have Gem Files extracted from them recursively using the same algorithm.

Each password brute-force attempt on each extracted file would cause the Gem to split into more Gem Files; like cutting the head off of a hydra, several more grow in its place!

A troublesome creature to summon, indeed! 🪄

User could supply a set of files to embed, and a password chain (one password for each nesting depth):

e.g. password chain: apple, kiwi, blueberry

At each nesting level, The Gem Files would be embedded in a random set of bits that is a random size relative to the available embed capacity.

The Gem Files would be encrypted with blueberry, then with kiwi, then embedded in the cover image using apple as the final/initial password.

In order to verify if a single password brute-force attempt was valid on a Gem Image, an attacker would then need to also brute-force the password/key of every random-looking Gem File extracted by the initial password brute-force attempt, recursively, until the number of bytes extracted from a Gem File are too small to try to extract from (or they find the hidden Gems).

To be extra sneaky, a user could first encrypt their files in an encrypted file container of some kind (that has no metadata that reveals its nature – the bits must appear random) and give it a filename of random characters.

That way, the only way to verify if the password guess is correct would be to know to look for and decrypt that file container, without any way of being able to tell it apart from any of the other random Hydra Gems.

As a bonus, when the correct password is entered, the real Gem File will be accompanied by a random number of gibberish Gem Files.

Ongoing Spell Research

These and other ideas are being explored in the development of new Gem Protocols and modes that can be selected when hiding or finding Gems.

Attacking HIDEAGEM

All security researchers are hereby cordially invited to test their magic against HIDEAGEM ! 🪄 ⚡

Perhaps I’ve made some humorous beginner’s mistakes, lol. I certainly made a ton along the way.

I’ll share my thoughts on some potential breaking conditions and directions for investigation.

Master Key Generation Early Exit

A means to reliably early exit on failed password brute-force attempts before generating the first Argon2id Master Key would render the initial key generation step fully broken.

HIDEAGEM’s initial key generation step takes special precautions to try to mitigate at least one kind of such attack.

Individual Cycle Key Slice Brute-Force Attacks

A means to individually brute-force any 256 bit slice of the Cycle Key (as it’s implemented in HIDEAGEM) would break the Cycle Key.

A core hypothesis is that the Cycle Key’s implementation in GEMMA_RANDOM is a demonstration of a 512-bit key and not two 256 bit keys. If it can be shown that any 256 bit key slice can be brute-forced individually, then that hypothesis would be disproven and the implementation of the Cycle Key broken.

The Cycle Key’s internal RNG is bootstrapped by seeding with the first 256 bits of the 512-bit key and is then immediately used to shuffle the key slice order vector.

In HIDEAGEM, immediately after creation the Master Key gets cycled several times in the process of initializing some random number generators and static keys.

This means that before the Master Key is used for the first time to select a random Ocean byte, the bits of the 256-bit key have been mutated by all 512 bits of the internal key.

Then, as the Gem is embedded/extracted, the Master Key is cycled to the next random 256-bit key slice each time it consumes >= 64 bytes of internal RNG output, Ocean bits, and Gem File bits, which works out to about 1 cycle every ~7 Ocean bytes (so in 1-bit mode, that is 1 cycle every 7 bits hidden in the Ocean).

Additionally, the Gem Stream (hidden bits read from the Ocean) has been designed with the objective of making it virtually impossible to determine if the key is valid until all of the Gem bits have been fully extracted, or the Ocean bytes to read from are exhausted.

Time Trap Early Exit / Bit Trap Mitigation

I’m particurarly interested to see if anyone can defeat my Time Trap.

It seems too good to be true, so I’m wondering if I missed something really obvious.

One potential attack I can think of involves steganalysis of the pixels/bytes the bit trap is read from. For example, if a lot of data is embedded in an image with a high bit mode like 7-bit, the bit trap bytes might stand out as it only writes up to 1 bit per byte.

For this reason, I’m considering corrupting the bit trap bytes at random in the same manner as the key salt bytes.

Another potential attack idea is to use steganalysis to terminate extraction beyond a certain number of bits collected, based on the probable message size.

Steganalysis

I don’t know a lot about the field of steganalysis yet, and have only done some simple tests so far.

Question: Does the extremely random nature of GEMMA_RANDOM provide any benefits to resisting steganalysis?

I’m curious to see if any steganalysis techniques, particularly machine learning-based methods that require training on a dataset of stego images created using a specific tool, can reliably detect if GEMMA_RANDOM specifically was used to embed a message.

Each Gem hide / find process is randomized by the password/key, image bits, Gem File bits, and true randomness.

The true randomness sources are the key salt bytes and the stego embed algorithm:

At every Ocean byte visited, the LSB matching insertion algorithm true randomly adds or subtracts from the Ocean byte to embed the data. That byte is then consumed by the Cycle Key, which influences the RNG that randomly selects the next Ocean byte to visit.

I suspect that bit modes > 1 bit per Ocean byte may leave a statistical imprint that’s distinct from LSB matching embedding that writes only to the first LSB.

Web Browser Extension / Add-on

The next thing I’d really like to work on is integrating HIDEAGEM into a browser extension so that it’s as accessible and easy to use as possible.

• Right click image
• Select ‘Hide A Gem’
• File chooser dialog opens: Select your Gem files
• The files are hidden and the Gem image is copied to the clipboard
• Paste the clipboard into an image editor or social media post

Gems could be found the same way, and the extension could do other things such as automatically search for Gems using a list of passwords when browsing images at specific URLs.

Gems could contain any data, including hidden web pages / apps that do fun things like reveal a hidden social media profile after extracting a Gem from an image in a post.

Final Thoughts

That’s all for now, I hope you enjoy my enchanted software! ✧(ꈍᴗꈍ)✧

To learn more about what inspired HIDEAGEM’s creation, warp to here. 🌌🐬

HIDEAGEM was written in Vim running in my terminal emulator UltraTerm, check it out!

The next steps are widescale user testing of HIDEAGEM v.1 and informal peer review of the implementation and design concepts discussed here.

I’d love to hear your feedback (and see any rare Gems that you mine)! ✨ ♊ 💎 ⛏️

Drop by the Discord server, visit me on Bird App X, or send me an email [email protected]

Donations Welcome ❤️‍🔥

If you love HIDEAGEM and any of my other software, videos, and independent research, please consider donating!

I want to continue making gifts for the world, and your contributions help a lot with that!

Terminology

The word random means pseudo random in all contexts, unless explicitly referred to as true random.

The acronym RNG (Random Number Generator) in all instances refers to a CSPRNG (Cryptographically Secure Pseudo Random Number Generator).

Cover Image/File: The image or other file type that will have data hidden inside of it.

Ocean / Bit Ocean: The bit collection, such as cover media, that the Gem bits will be hidden inside of.

Gem (or Gem File): Any file or data being hidden by the user.

Gem Protocol: Defines the Gem hide/find procedure and stego algorithm.

Gem Hide: Process of hiding/embedding Gem in cover image.

Gem Find: Process of finding/extracting Gem from cover image.

Gem Data: Any bits hidden in the cover image.

Gem Stream: A series of Gem Shards that are to be written to / read from the Ocean.

Gem Pixel: A pixel that has Gem data hidden inside of it.

Gem Trail: The locations and sequence of Gem Pixels the Gem data is stored in.

Gem Image: The cover image after being mutated by the Gem Hide process.

How to Use HIDEAGEM

With ComfyUI

To use HIDEAGEM with ComfyUI for Stable Diffusion , just extract the archive to the custom_nodes directory and look for the HIDEAGEM nodes in the right-click context menu. There are examples of how to use the nodes in the workspaces folder.

🚨 WARNING: ComfyUI’s save image node reveals that HIDEAGEM was used in the PNG metadata !!!

Use HIDEAGEM’s SAVE IMAGE node: It doesn’t save that metadata to the output Gem image! 💎✨

NOTE: The hide and find nodes don’t handle images with an alpha channel (such as transparent PNGs) properly. For now, use HIDEAGEM via the CLI if you need to hide/find Gems in images that have alpha channels.

Hiding Gems

HIDEAGEM can hide Gems (files) inside of any other file, which HIDEAGEM calls a bit Ocean.

HIDEAGEM will try to detect if the input Ocean is an image file, and if so will use only the image’s pixel bytes as the bit Ocean. The rest of the image file will be completely discarded and the Gem image will be saved to the specified output directory as a .png image with the same file name as the input image.

To hide a Gem, just pass HIDEAGEM an Ocean, one or more Gem Files, and a password. If no output directory is specified, then the Gem hide will proceed but the output won’t be saved to disk.

python HIDEAGEM.py hide --ocean MORIA.JPEG --files RUBY.TXT EMERALD.TXT SAPPHIRE.TXT --output gem_images/ --password mellon

The Gem text files will be hidden inside of the pixel bytes copied from MORIA.JPEG, and the resulting Gem image MORIA.PNG will be saved to the directory gem_images.

If an RGBA image is used as the Ocean, the alpha channel bytes and the RGB bytes of any fully transparent pixels will not be written to.

Finding Gems

Finding Gems is simple ( if you have the password ! ):

python HIDEAGEM.py find --ocean MORIA.PNG --output gem_images/ --password mellon

HIDEAGEM will search for Gems in the Ocean MORIA.PNG with password “mellon” and if any are found save them to gem_images.

If Gem find is run without an output directory, the Gem Files will be extracted (if found) but nothing will be saved to disk.

Hiding / Finding Time Trap Gems

WARNING: Experimental feature !!! Use at own risk !

HIDEAGEM can place a Time Trap enchantment on Gems so that it’s harder to brute-force the password.

Time Traps have a level from 0 to 7 that changes how long it takes to extract the Gem and verify the password.

Level 0 has no addtional time added: Gem embedding and extracting takes the same time as without a Time Trap.

Levels 1 - 7 have longer extraction times, with 1 being the shortest and 7 the longest.

When the correct password is entered, the Gem is extracted using the Time Trap level specified when hiding the Gem.

When an incorrect password is entered, a random Time Trap level is fished from the Ocean with a high probability of catching the slowest one:

LEVEL 7 = 50%      (1/2)
LEVEL 6 = 25%      (1/4)
LEVEL 5 = 12.5%    (1/8)
LEVEL 4 = 6.25%    (1/16)
LEVEL 3 = 3.125%   (1/32)
LEVEL 2 = 1.5625%  (1/64)
LEVEL 1 = 0.78125% (1/128)
LEVEL 0 = 0.39062% (1/256)

Around half of password brute-force attempts will select level 7, no matter which level was used to hide the Gem (even level 0).

It’s possible to hide Gems that take less than a second to extract, but take several minutes to attempt a single password brute-force attempt on.

The price of the Time Trap is convenience: Accidentally entering the wrong password can cost a lot of time, so it’s not suitable for use in contexts where immediate wrong password feedback is required.

Hiding a Time Trap Gem

To add a Time Trap to a Gem, just add the --timetrap flag, with an optional level from 0 to 7 (if none is specified, 0 is selected):

python HIDEAGEM.py hide --ocean MORIA.JPEG --files DIAMOND.TXT --output gem_images/ --password mellon --timetrap [level]

Finding a Time Trap Gem

To find a Time Trap Gem, just add the --timetrap flag (no need to include the level):

python HIDEAGEM.py find --ocean MORIA.PNG --output gem_images/ --password mellon --timetrap

Note that HIDEAGEM find does not automatically look for Time Trap gems unless asked to.

Demo Mode & Unit Tests

If you want to watch HIDEAGEM generate random Gem Seals by hiding random data in a random Ocean, you can run demo mode:

python HIDEAGEM.py demo

If you want to see HIDEAGEM hide and find Gems as fast as it can, you can run some unit tests:

python HIDEAGEM.py unit

Press CTRL + C to exit both modes.

Technical Notes

HIDEAGEM is an experimental tool for hiding files inside of images.

It’s written in C++ and can be used via Python CLI and custom nodes in ComfyUI for Stable Diffusion.

WARNING: HIDEAGEM is experimental software! It may have unknown flaws or vulnerabilities. Use at own risk!

WARNING: HIDEAGEM has not yet been studied to determine its resistance to steganalysis (e.g. tools that calculate the probability of a hidden message being present in an image). So assume that it may be possible for adversaries to detect if an image is “suspicious.”

Objectives

Steganography is about hiding the presence of a message; it’s about concealing the existence of communication.

HIDEAGEM aims to be a next-generation steganography platform, combining modern cryptographic and steganographic techniques in order to facilitate fast, secure, and robust information hiding in cover media.

In addition to pursuing the traditional objective of steganography (stealth communication), other security properties of hiding message bits in large bit collections are being explored.

Steganography Platform

HIDEAGEM is designed to be expandable and adaptable, a platform from which various steganographic algorithms and techniques can be launched to conceal data within a variety of cover media types.

New stego algorithms can be incorporated into the program over time in order to support more file types and leverage new techniques.

Features

List of general features and potential future development directions.

Current Features               |  Future Development
-------------------------------|---------------------------------------------------
Unicode passwords              |  Keyfiles
Tamper-proof Gem data          |  Mobile app
512-bit symmetric key          |  More stego algorithms
Secure Memory Handling         |  More cover media types
Multiple files per password    |  Split files across images
Multiple passwords per image   |  Web app (local execution)
Offline brute-force resistance |  Browser extension (e.g. context menu Gem extract)

Unicode Passwords

Use any crazy Unicode characters you want in your passwords: You can even use your favorite emojis; no one can stop you! 🐬

Tamper-Proof Gem data

Note: The information below applies only to HIDEAGEM’s current spatial domain algorithms that are compatible only with lossless image formats such as PNG, TIFF, and BMP.

If a Gem is successfully extracted and has the correct Gem Hash, then it is virtually guaranteed to be bit-for-bit the same Gem that you hid in the image.

If even a single bit of a Gem Pixel (a pixel that has Gem data hidden inside of it) is corrupted then the Gem extraction will fail.

Tamper-proof comes at the cost of fragility: Small changes to Gem Images can make the data unrecoverable. They are fragile and can be broken by resizing, cropping, or mutating a pixel that contains Gem data.

512-bit Symmetric Key

HIDEAGEM uses an experimental symmetric key system designed to work in concert with its steganographic algorithms.

The 512-bit key is generated using libsodium’s Argon2id password hashing function and the user supplied password.

Argon2id was selected because it offers configurable brute-force resistance parameters (such as memory requirements), and resistance to GPU brute-force attacks.

The Gem data is encrypted using a 256-bit key derived from the 512-bit key, and is then hidden in the cover media using the 512-bit key. The 512-bit key must first be used to extract the entire encrypted Gem before the 256-bit key can be used to decrypt any of its bits.

You can learn more about the key system here.

NOTE:  The key's ultimate strength is only as strong as the password. A very
       long/random password is required to leverage all 512 bits of the key.

       To achieve 512 bits of entropy with a password using the ASCII character set,
       the password would have to be >= ~74 chars and each character perfectly random.

Secure Memory Handling

In order to try to mitigate potential side-channel attacks, libsodium’s low level memory management functions are used to securely erase memory of keys, Gem files, and other sensitive data generated during the embed/extract processes.

It’s also used to prevent sensitive data like keys from being swapped to disk.

Multiple Files Per Password

You can think of images as encrypted write-once file folders or archives.

You can hide any number of files in an image using a single password, limited only by the image’s embed capacity. They’ll all be extracted at once when the correct password is entered.

The Gem Stream has an overhead of 52 bytes, and each Gem File an overhead of 8 bytes.

HIDEAGEM tries to compress all Gem Files with miniz (zlib) before encrypting them, which can sometimes reduce the number of bytes embedded substantially.

The max file size per Gem File and max bytes that can be embedded per Ocean is 16 exabytes.

Multiple Passwords Per Image

HIDEAGEM currently supports hiding multiple sets of files using multiple passwords and a single image, however a UI hasn’t been developed for using that feature yet.

The way it works is also a bit peculiar in that it’s hierarchical: To access the next set of files you need all the passwords that came before it in addition to the file set’s password.

So consider this a stealth feature that’s probably not useful yet.

MAGIC AI LICENSE [ MAGIC-AL ]

I created this license as an alternative to the “NO-AI” licenses that have appeared.

It grants permission to train generative AI models on the work so long as the models produced are made freely available for download by users of any system that serves them (for example, websites run by companies like Open AI and Google that serve access to LLMs and AI 2D image generation).

This is so that users can run the models on their own hardware if they’d prefer, or use the model via another service provider.

The MAGIC-AL license transfers to derivative works of the licensed work, so if something licensed under MAGIC-AL is modified, that version is also MAGIC-AL.

NOTE: I’m not a lawyer and have no idea if this could work!

Magical Contingency License

I’m of the position that trying to restrict what IP generative AI models can be trained on (and/or what the models can be used for afterwards, such as for commercial video game development) cannot be done without creating a nightmare for everyone.

If in the unfortunate event micro-managing the IP rights of every shred of data used to train generative AI models becomes the industry standard, perhaps data licensed under MAGIC-AL could help encourage access to more open source models, and lead to having a greater number of AI service providers to choose from.

The objective is to promote open source generative AI models, as well as to make a point:

A license like this, and by extension any licenses granting/forbidding training on a licensed work, are not enforceable.

At least, not without a radical and intrusive transformation of how intellectual property licensing is tracked and managed, which may very well be what is being proposed by major corporations such as Adobe and Publicis Groupe.

C2PA Quick Rundown

The stated objectives of Adobe’s content surveillance platform C2PA appear to be two-fold:

• Manage intellectual property rights during “the use” (and presumably creation) of generative AI models (and other contexts).

• Surveil and censor the output of generative AI models online (and other things, such as cameras) in order to stop “mis/disinformation” from confusing the public.

From what I can gather by reading their papers, the plan is to track all media content online by embedding e.g. images with invisible watermarks using AI steganographic algorithms. The watermarks are to either include a bundle of cryptographically signed metadata called a C2PA manifest, or a key that retrieves the metadata from a “C2PA manifest repository.”

These AI steganographic watermarks are apparently quite robust, in that they can survive a lot of image mutation. One company Steg.ai calls it an “invisible QR code” and they claim the C2PA key can be read using a cellphone camera pointed at a monitor that’s displaying a watermarked image (HIDEAGEM doesn’t have cool magic like that – yet!).

Using perceptual hashes of images as keys to retrieve the C2PA surveillance data from the centralized repositories (run by e.g. news corporations and intellectual property management firms) was also suggested, so that that the C2PA metadata can be restored in the event all of the stego data was destroyed (such as by mutating the image beyond its limits).

Of note, it appears that Adobe’s meetings are sometimes visited by representatives from the US Military who see C2PA’s widescale adoption as potentially advantageous for general Internet surveillance.

Whether or not this brazen scheme will successfully entrench itself based on copyright-related matters remains to be seen.

Right now, it looks like Adobe is introducing C2PA metadata into their software ecosystem, and that there’s an influence campaign being run to try to convince creators to adopt C2PA, both to “protect” their work, and to prove that their use of AI is “ethical.”

All the while, the “AI disinformation” side of the C2PA bandwagon is quietly defining how our future computers will operate, with support for C2PA watermarking at the hardware level in mobile processors being recently announced by Truepic and Qualcomm.

The one thing team C2PA seems to have going for them, is that hardly anyone is paying attention to what they’re up to.